递归与尾调用优化

发表于 | 分类于

一、如何理解递归

递归是一种算法，或者说是一种编程技巧。思路是将大规模的问题划分为另一个或者多个小规模的子问题。子问题继续划分为更小的子问题，直到最小的问题能一眼看出结果。由大问题化小的过程就是“递”，由小问题的结果一步步计算大问题的结果的过程就是“归”。

二、递归需要满足的条件

什么样的问题可以用递归的思路解决，需要满足如下三个条件：

  • 一个问题的解可以分解为一个或者多个子问题的解。
  • 这个问题与分解后的子问题，除了数据规模外，求解思路完全一样。
  • 存在某一个足够小的子问题能一眼看出答案，即存在递归的终止条件。

三、如何理解运用递归

递归中的问题一步步拆解向下，再一步步返回结果是对计算机友好的，因为计算机最擅长做的就是重复性的工作。但对人来说则不一样，一层层往下子问题越来越多，人脑试图分析记住所有的情况就相对困难。

所以人在分析递归问题是，要假设分解的子问题已经解决，再次基础上思考如何解决大问题。且只要分析一层的分解关系，无需一层层往下思考。屏蔽掉递归细节。

递归的关键就是找到将大问题分解为小问题的规律，并基于此分析递归公式，然后找出终止条件。其它的细节不必考虑。

四、递归存在的问题

4.1 堆栈溢出

递归解决问题的思路决定了当问题规模较大的时候，递归过程中就会有大量的函数调用。而每一次函数调用都伴随着栈帧入栈的过程。所以递归很容易出现堆栈溢出问题

如下这个简单的递归函数：

1
2
3
4
int f (int n) {
    if (n == 1) return 1;
    return f(n - 1) + 1;
}

当jvm参数 -Xmx 为10M时，n取值超过12W，就会出现StackOverflowError等问题。

解决思路：

1.增加深度判断拦截，防止计算层级过深，比如限制10W层级，代码修改如下：

1
2
3
4
5
6
7
int f (int n) {
  	if (n=100000) {
      	throw new IllegalArgumentException("scale of data too large");
    }
    if (n == 1) return 1;
    return f(n - 1) + 1;
}

2.采用尾调用优化（下面会讲到）

4.2 重复计算问题

我们看一下fibonacci计算的递归函数：

1
2
3
4
5
6
int fibonacci(int n) {
  	if (n == 1 || n ==2) {
      	return 1;
    }
    return fibonacci(n - 1) + fibonacci(n - 2);
}

假设n为5，分析一下调用过程: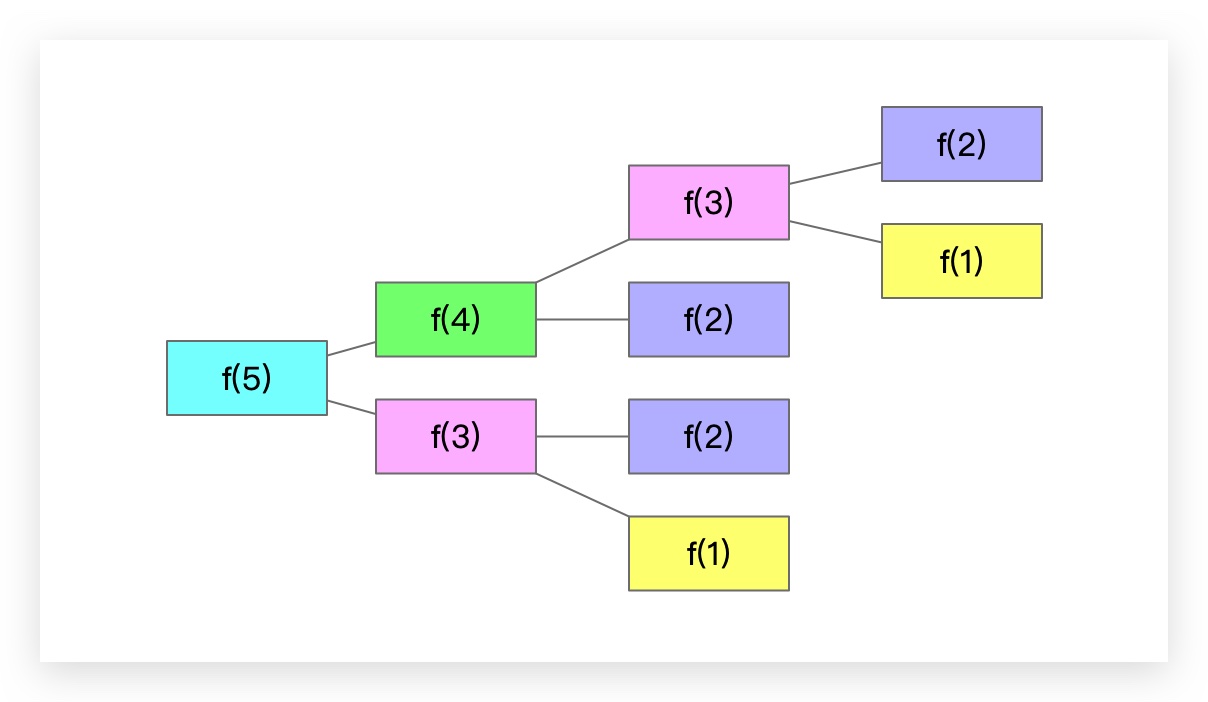

可以看到 计算 f(5)，分别计算了 f(4)一次，f(3)两次，f(2)三次，f(1)两次。其中有很多重复计算的情况。

解决思路

可以使用一个中间结果的容器（比如map）将计算的中间结果缓存起来，下次计算之前先取缓存，不存在再计算。会大量减少计算的次数。

五、尾调用优化

5.1 什么是尾调用

一个函数的最后一步是调用另一个函数。比如：

1
2
3
int f(int n) {
	return g(n + 1);
}

下面这样就不属于尾调用：

1
2
3
int f(int n) {
	return g(n) + 1;
}

5.2 尾调用优化

我们知道每一步的函数调用都伴随着栈帧的入栈，每一次的函数返回都伴随着栈帧的出栈。

之所以要入栈，是为了保存外层函数的中间状态，再内层函数返回后能继续外层函数的执行。

那如果内存函数是外层函数的最后一步，外层函数已经没有其他中间变量状态需要保存，外层函数的返回完全依赖内层函数的返回值，那么我们就没有必要使用栈帧保存外层函数中间状态了。也就减少了内存的消耗。

由于递归常常伴随着大量的函数嵌套调用，所以这种优化的技巧在递归的场景下作用尤其明显。

5.3 如何编写尾调用的递归代码

技巧就是把函数的返回值（累加值）作为参数一层层传递下去，看一个例子：

1
2
3
4
int f (int n) {
    if (n == 1) return 1;
    return f(n - 1) + 1;
}

其中有一个内部变量 1，我们想办法把它挪到参数列表中：

1
2
3
4
int f2(int n, int total) {
    if (n == 1) return total + 1;
    return f2(n - 1, total + 1);
}