这两种排序的思想都是采用分治思想解决问题。将时间复杂的降到 O(n log n ),放到一起进行总结。
一、n*log n 中 log n 的由来
为什么采用分治的思想解决问题时,往往会出现log n这样的特殊计算式。分析一下原因,下面是规模为N的一个任务的拆解: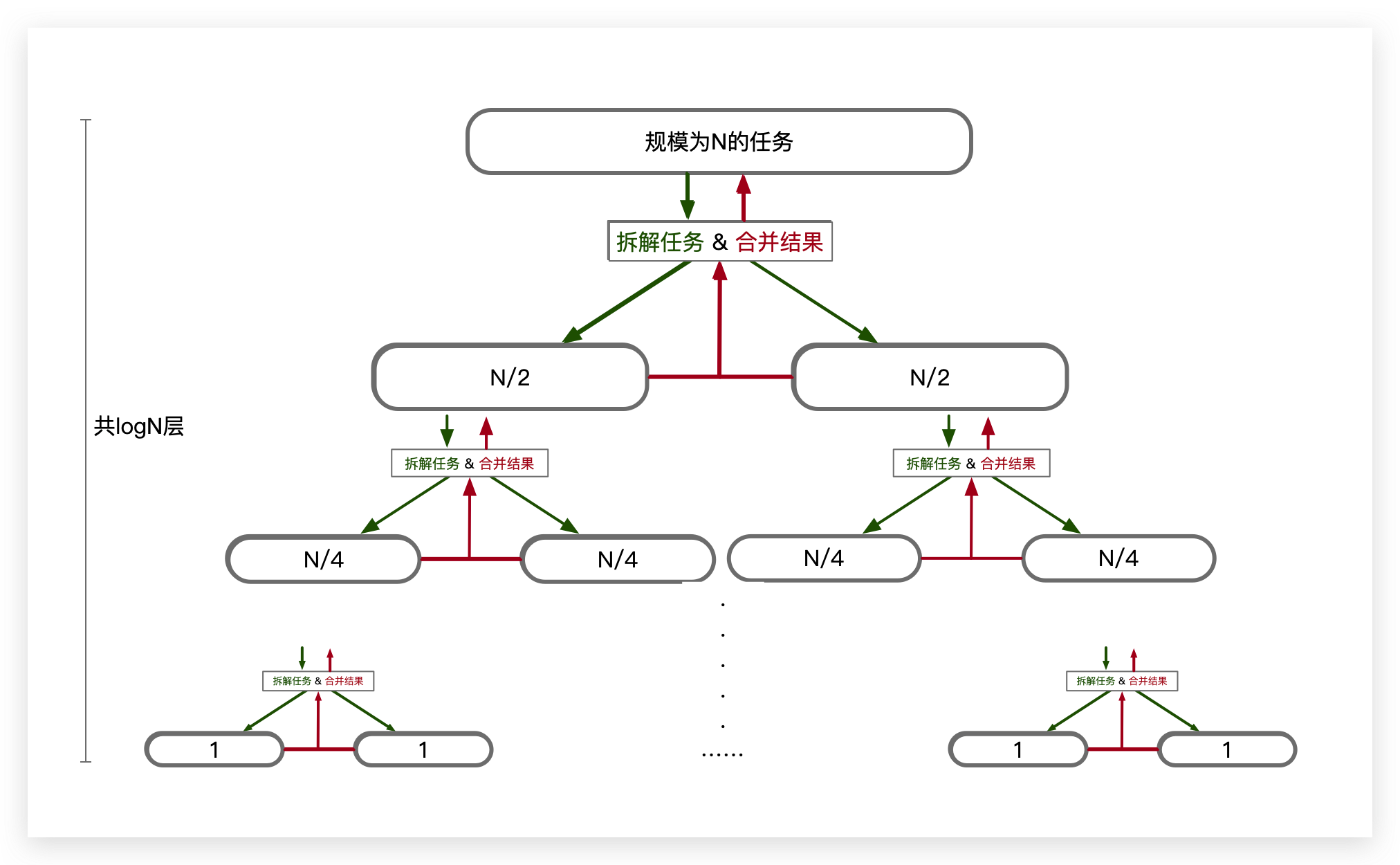
每往下进行一层拆解,大任务被拆分为两个子任务,再最下一层,任务被拆解到了规模为1的任务。其中各层拆解过程中的计算为两个方面:
- 如何拆解任务。
- 如何合并任务。
所以整个任务的时间复杂度为 每一层计算(拆解+合并)的和 加上 最终所有最小规模任务的计算时间复杂度。
而一个叶子节点为N个的二叉树的树高为 log n。假设每一层计算(拆解+合并)的时间复杂度为T(n)。最小规模任务已经和n无关,假设每一个最小任务时间为常量S。
则最终复杂度为:T(n) * log n + S * n。这里就是常出现的log n的由来。
归并排序&快排,就是把上述的T(n) 控制在了O(n), 来保证最终的时间复杂度为 O(n * log n )。
二、归并排序
2.1 核心思路
先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。
拆解策略:将数组从中间分为前后两部分。(利用数组的按下标随机访问的特性,常量时间内办到)
合并策略:将了两个有序的数组合并为一个有序数组。
最小规模任务:对只有一个元素的数组进行排序。(无需进行)
所以难点就在合并策略上。
2.2 合并策略
要合并两个有序数组 Array1,Array2。可以开辟一块新的内存空间,长度为length1+length2。依次从头遍历两个数组,用两个游标 i 和 j,分别指向 Array1和 Array2 的第一个元素。比较这两个元素 Array1[i]和 Array2[j],如果 Array1[i]<Array2[j],我们就把 Array1[i]放入到临时数组 tmp,并且 i 后移一位,否则将 Array2[j]放入到数组 tmp,j 后移一位。
2.3 时间复杂度分析
根据第一节的分析。拆解任务时间复杂度常量级;根据合并策略的描述,容易分析合并任务时间复杂度为 O(n);最小规模任务的时间复杂常量级。
所以总的时间复杂度为:O(n * log n) +O(n) = O(n * log n)。
2.4 空间复杂度分析
由于合并任务中需要申请新的内存空间,最大数组长度n即可。所以时间复杂度为 O(n)。
2.5 稳定性分析
由于合并时能控制两个元素相等时的合并策略,从而保持相等元素的相对位置,所以归并排序是稳定的。
三、快速排序
3.1 核心思路
一个长度为n的数组(下标0~n-1),选择数组中任意一个元素作为pivot,将数组中小于pivot的元素放到该元素左边,数组中大于pivot的元素放到该元素右边。数组被封为三部分,前面第一部分都是小于 pivot 的,中间第二部分是 pivot,后面第三部分都是大于 pivot 的。接下来用同样的策略保证第一和第三部分有序,则整个数组有序。
拆解策略:选择数组中任意一个元素作为pivot,将数组中小于pivot的元素放到该元素左边,数组中大于pivot的元素放到该元素右边。左右即拆解为两个子任务。
合并策略:在原数组中进行,无需特别合并。
最小规模任务:对只有一个元素的数组进行排序。(无需进行)
所以难点就在拆解策略上。
3.2 拆解策略
选取最后一个元素(下标n-1)作为pivot,使用两个游标i,j,依次从下标0至下标n-2遍历整个数组。保证遍历的部分满足按小于pivot 和 大于等于pivot 分为两块。i始终指向已处理区间中第一个大于等于pivot的元素(即第二块第一个元素,标明分界点)。而j始终指向已处理元素的最后一个(标明进度)。
有一种个情况下i会指向小于pivot的元素,即已处理的元素都是小于pivot的,这时候i和j一起指向已处区间的最后一个
每处理一个新元素,如果待处理元素大于pivot,i不动,j后移一位。如果小于pivot,将新元素与i指向的元素交换,i,j均后移一位。
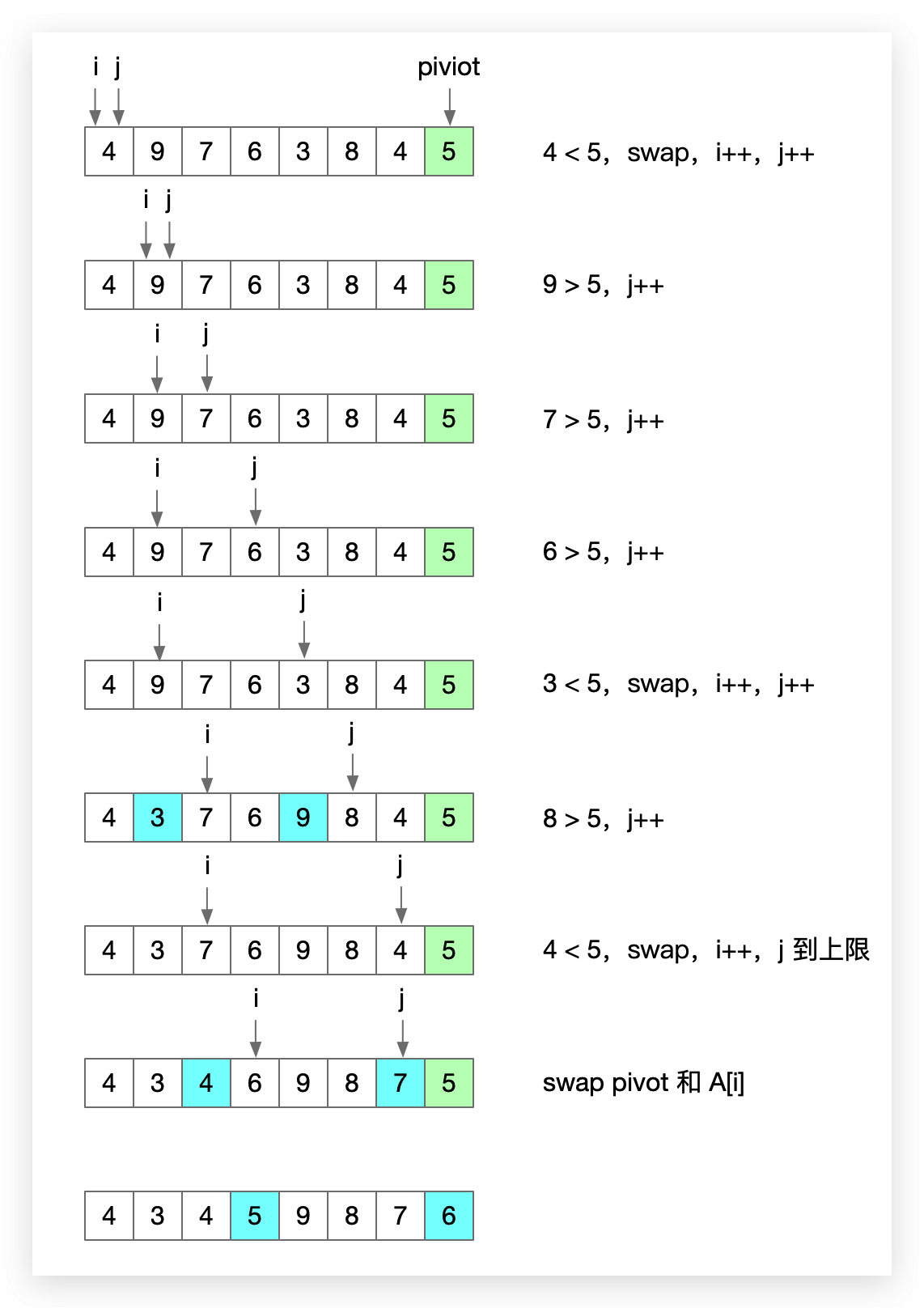
3.3 时间复杂度分析
根据第一节的分析。合并任务时间复杂度常量级;根据拆解策略的描述,容易分析拆解任务时间复杂度为 O(n);最小规模任务的时间复杂常量级。
所以总的时间复杂度为:O(n * log n) +O(n) = O(n * log n)。
3.4 空间复杂度分析
由于拆分任务无需申请新的空间,故空间复杂度为O(1)。
3.5 稳定性分析
由于拆分时涉及到非相邻元素的交换,可能会改变相等元素的相对位置,故快排是非稳定的。
四、归并排序 & 快速排序 对比
| 归并排序 | 快速排序 | |
|---|---|---|
| 时间复杂度 | O(n * log n) 得益于合并任务O(n) |
O(n * log n) 得益于拆解任务O(n) |
| 空间复杂度 | O(n) 非原地排序 |
O(1) 原地排序 |
| 稳定性 | 稳定 | 非稳定 |