树

发表于 | 分类于

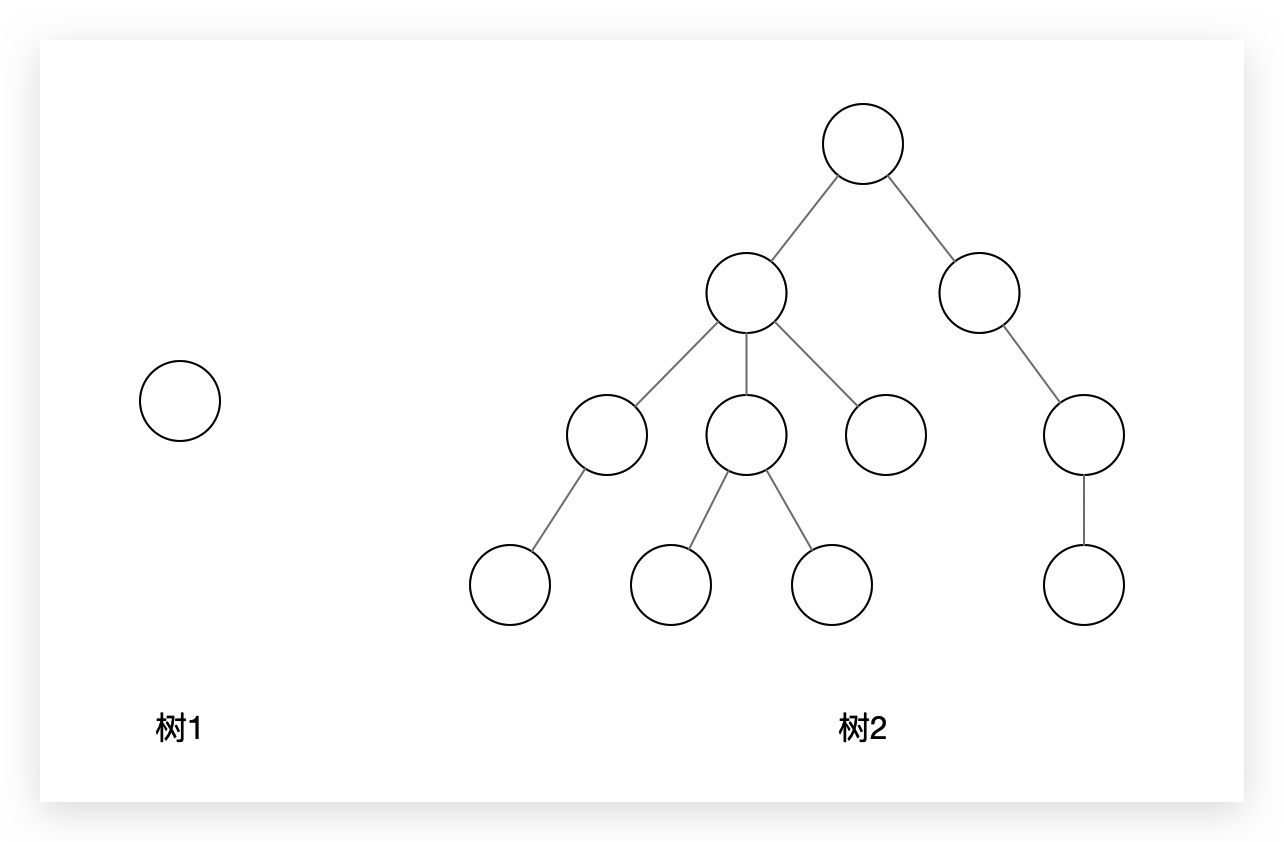
1.树的定义

树可以用如下的方式递归的进行定义

树是n(n>=0)个结点的有限集。它

（1）或者是一棵空树（n=0），空树中不包含任何结点

（2）或者是一棵非空树（n>0），此时有且仅有一个特定的称为 根（root） 的结点；当n>1时，其余结点可以分为m(m>0)个互不相交的有限集T1,T1,…,Tm，其中每一个本身又是一棵树，并且称为根的 子树（sub tree）

如上的定义形式并不直观，如下有一些树的示例。

1

2.树的相关概念

  1. 根节点：没有父节点的节点。
  2. 叶子节点：没有子节点的节点。
  3. 节点高度：节点到叶子节点的最长路径。
  4. 节点深度：根节点到这个节点的路径长度。
  5. 节点层数：节点深度+1。
  6. 书的高度：根节点的高度。

3.二叉树

每个节点最多只有两个子节点。一些特殊的二叉树：

满二叉树：叶子节点全部在最底层，除叶子节点外，每个节点都有左右两个子节点。

完全二叉树：叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，除了最后一层，其他层的节点个数都要达到最大，这种二叉树叫作。

3.1 二叉树的存储方式

链式存储法

一个节点item的对象定义一般如下：

1
2
3
4
5
pulic class TreeItem<T> {
	private TreeItem leftChild;
	private TreeItem rightChild;
	private T value;
}

顺序存储和法：

使用数组存储二叉树。根节点存储在下标 i = 1 的位置，左子节点存储在下标 2 i = 2 的位置，右子节点存储在 2 i + 1 = 3 的位置。以此类推。

2

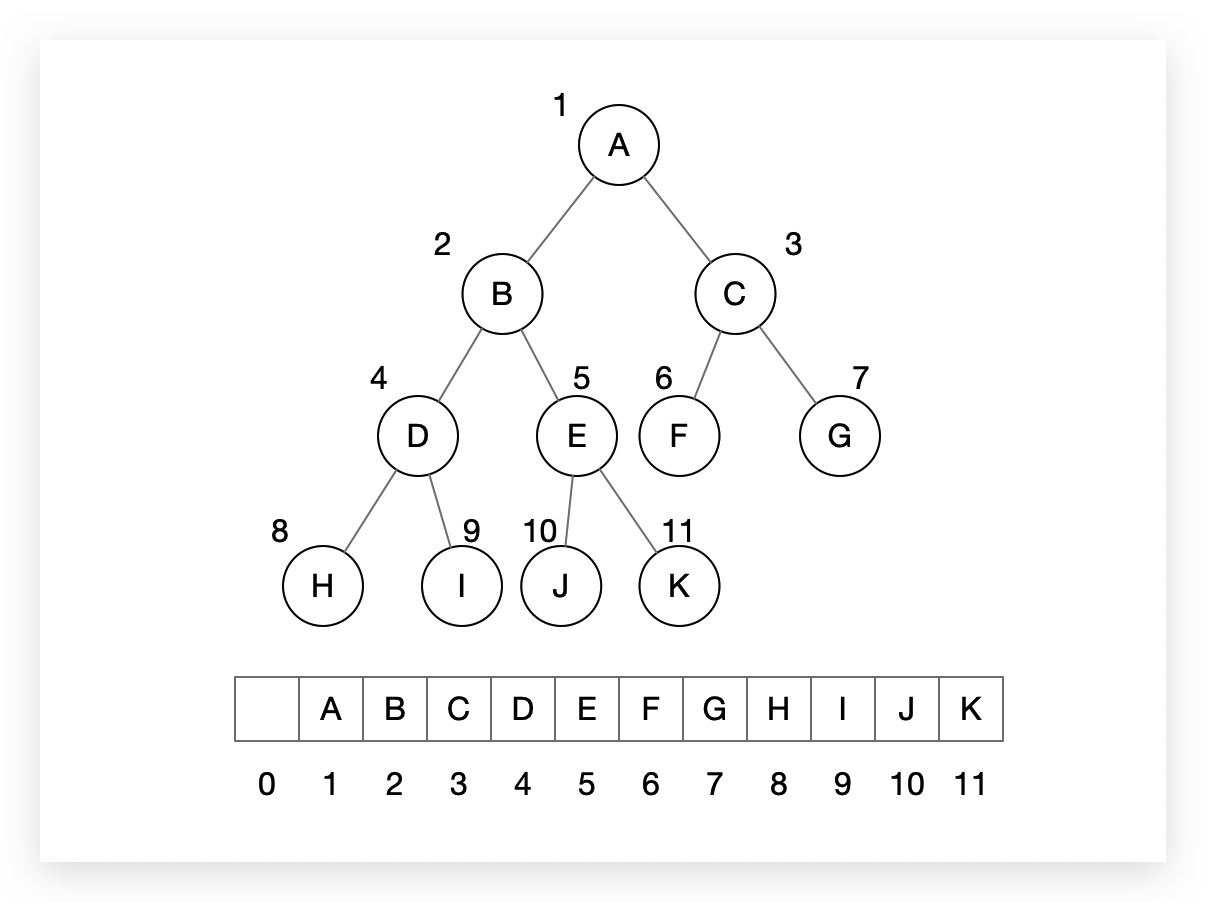
如上是一颗完全二叉树的存储结构，为了方便计算，浪费了0下标的存储空间。

如果是一颗非完全二叉树，那么浪费的空间会更多，这就是完全二叉树的一个优势。

3.2 二叉树的遍历

比较常见的遍历方式有三种，前序遍历、中序遍历、后序遍历。前、中、后指的是某个节点和其左右子树的遍历排序。

  • 中序遍历：左子树→父节点→右子树。
  • 前序遍历：父节点→左子树→右子树。
  • 后序遍历：左子树→右子树→父节点。

4.二叉查找树

一种特殊的二叉树，在树中的任意一个节点，其左子树中的每个节点的值，都要小于这个节点的值，而右子树节点的值都大于这个节点的值。

4.1 二叉查找树的基本操作

元素的插入：从根节点开始，依次比较要插入的数据和节点的大小。如果要插入的数据比节点的数据大，并且节点的右子树为空，就将新数据直接插到右子节点的位置；如果不为空，就再递归遍历右子树，查找插入位置。同理，如果要插入的数据比节点数值小，并且节点的左子树为空，就将新数据插入到左子节点的位置；如果不为空，就再递归遍历左子树，查找插入位置。

元素的删除：

  1. 情况一，如果要删除的节点没有子节点，我们只需要直接将父节点中，指向要删除节点的指针置为 null。比如图中的删除节点 55。
  2. 情况二，如果要删除的节点只有一个子节点（只有左子节点或者右子节点），我们只需要更新父节点中，指向要删除节点的指针，让它指向要删除节点的子节点就可以了。比如图中的删除节点 13。
  3. 情况三，如果要删除的节点有两个子节点，这就比较复杂了。我们需要找到这个节点的右子树中的最小节点，把它替换到要删除的节点上。然后再删除掉这个最小节点，因为最小节点肯定没有左子节点（如果有左子结点，那就不是最小节点了）。

元素的查找：先取根节点，如果它等于我们要查找的数据，那就返回。如果要查找的数据比根节点的值小，那就在左子树中递归查找；如果要查找的数据比根节点的值大，那就在右子树中递归查找。

二叉查找树能在O(height)的时间复杂度下完成元素的增、删、查。

4.2 二叉查找树支持的其它操作

  • 查找某个节点的前驱节点、后继节点。
  • 查找所有节点中的的最大、最小节点。
  • O(n)时间复杂度，输出所有节点的有序序列（中序遍历二叉树）。

4.3 二叉查找树中如何处理重复元素

方法一：通过链表和支持动态扩容的数组等数据结构，把值相同的数据都存储在同一个节点上。

方法二：把后一个要插入的等值数据当做大于这个值处理。相应查找和删除都需要做改变。

4.平衡二叉查找树

前一节提到二叉查找树的基本操作能在O(height)时间复杂度下完成。

height 的范围在log(n)（满二叉树）- n（退化为链表的情况）。

平衡二叉树的出现就是为了保证树高不会过高。平衡二叉树的严格定义：

二叉树中任意一个节点的左右子树的高度相差不能大于 1

4.1 红黑树并不“平衡”

说红黑树不“平衡”是针对严格的平衡定义的，而红黑树从根节点到各个叶子节点的最长路径，有可能会比最短路径大一倍。即最大树高在某些情况下会退化到严格定义下的树高的两倍。但这并不影响红黑树的高效。

4.1 红黑树 vs AVL树

AVL树和红黑树都是平衡二叉树（非严格平衡）。

  • 插入操作：都是至多两次旋转。
  • 删除操作：AVL 最坏情况下O(logN)，而红黑树最多只需3次旋转，O(1)复杂度。
  • 查找：由于红黑树的平衡是非严格的，而AVL是严格平衡的。所以查找效率的时间复杂度，AVL树是 O(logN)，而红黑树是 2O(logN) 。

总结起来，红黑树的查询性能略微逊色于AVL树，但红黑树在和删除上要高效很多。