我们知道二分查找的效率非常高,一次对比就能将元数据规模缩小一半,最终在O(logn)的时间复杂度内完成有序数组中的特定元素查找。二分查找有一个局限是只能在数组完成该操作,因为其强依赖按下标的随机访问。需要按下标快速定位到中间元素。
如果数据存储在链表中,如何利用二分的思想完成数据查找呢?这种结构就是跳表。
1.什么是跳表
我们知道在一个有序链表中查找元素,只能从头开始一一对比,直至找到元素。例如在如下链表中查找元素21。
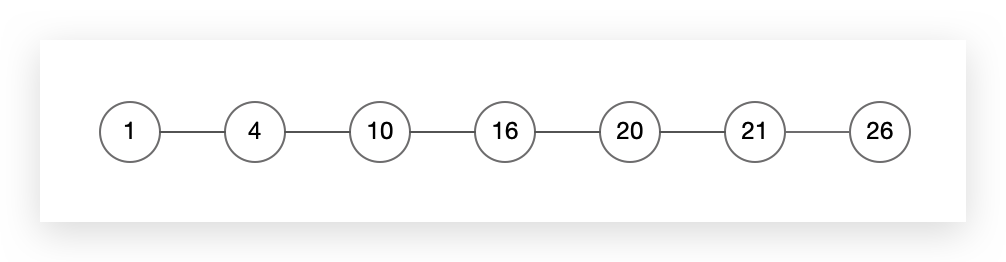
如果不做特殊处理,那么查找路径如下,时间复杂度是O(n)。
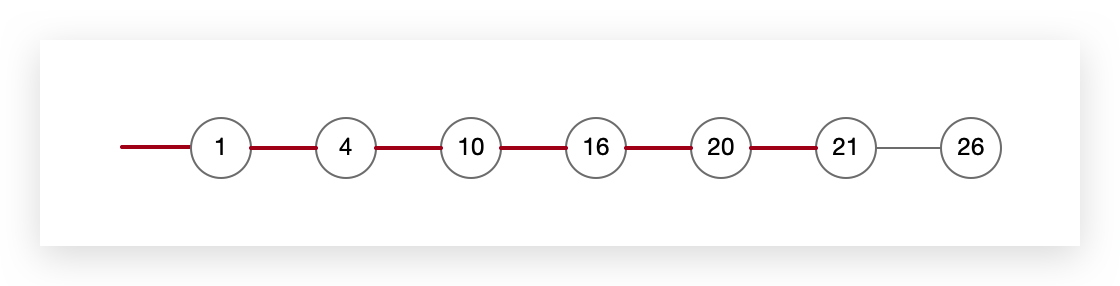
现在我们给这个链表加一层索引,通过这个索引能快速的定位到中间的元素。那么通过一次对比,就能将数据规缩小一半,对于剩下的数据在采用逐一对比的方法。
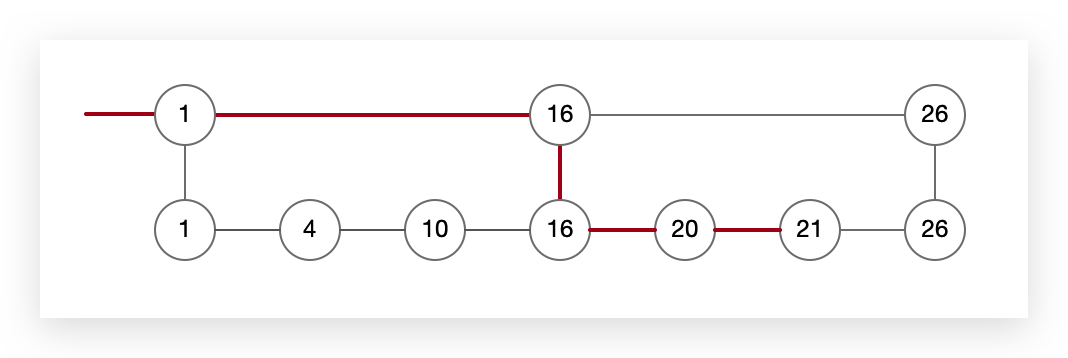
经过上述的优化,一次对比能将数据规模缩小一半,但对于余下的数据还是需要逐一对比,效率还是很低。解决方式就是对于余下的数据我们也加一层二分索引,于是就有了第二层索引。这样余下的数据也通过二分的思想提高了查找效率。
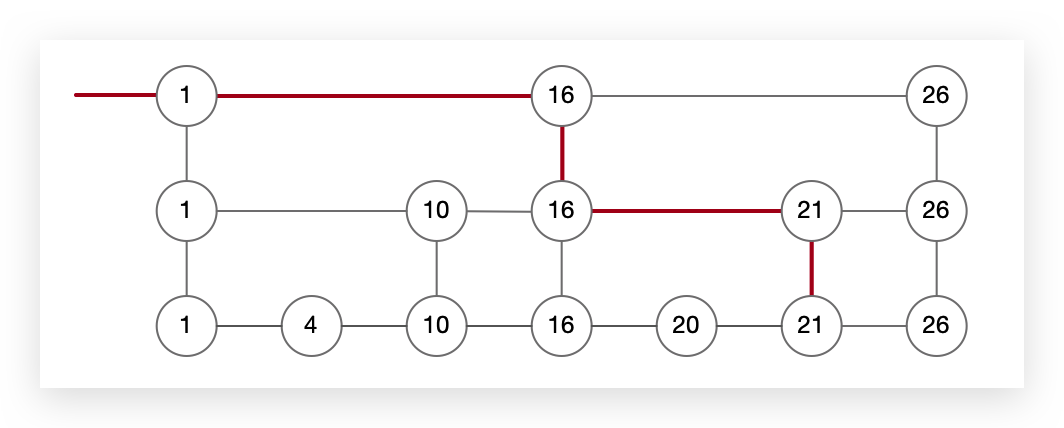
如果我们一直添加索引层,直至最下层索引的节点个数是原数据的一半,即每两个原数据就有一个索引与之对应。这样就构成了跳表。
2.跳表查询操作的时间复杂度
跳表的元素查找的时间复杂度是多少呢?
由于我们选择每两个元素就提出一级索引,索引每次对比操作都能将数据规模缩小一半,于是可以很快的分析出查找特定元素的时间复杂度是O(logn)。
3.跳表的额外空间占用分析
有得必有失,跳表能在链表的基础上大幅提高元素的查找效率,是以牺牲存储空间为待拣的。这个代价有多大呢?
额外的存储空间主要用来存储索引节点,还是以每两个数据节点抽一层索引为例。
则额外的索引节点数为:
|
|
利用等比数列求和,得到和为 n-2。大约要多耗费一倍的存储空间。
但在实际开发中,额外的消耗要比一倍小得多,因为在实际的开发中,原始链表中存储的是很大的对象,而索引结点只需要存储关键值和几个指针,而非整个对象,所以当对象比索引结点大很多时,那索引占用的额外空间就可以忽略了。
4.跳表的插入与删除
由于跳表的数据查找时间复杂度是O(logn),而跳表的底层数据结构是链表。单纯的插入和删除一个元素的时间复杂度是O(1)。
所以跳表的 “找到合适位置并 插入 一个元素” 的整体时间复杂度就是 O(logn)。
再来看删除操作,这里有些不一样,因为一个元素如果也出现在索引中,还需要同步的删除索引中的节点。
4.1 跳表索引的动态更新
如果对于删除操作,我们需要同步删除索引中的节点。那么对于插入操作,我们是否需要去维护索引也同步去添加这个节点呢?
如果我们不更新索引,就可能出现某 2 个索引结点之间数据非常多的情况。极端情况下,就退化成单链表。查找、添加、删除元素的性能都会下降。
所以我们需要某种策略取防止这种退化的发生。
当向跳表中插入数据时,可以选择同时将这个数据插入到部分索引层中。具体哪一层是通过一个随机函数来决定,随机函数生成了值 K,就将这个结点添加到第一级到第 K 级这 K 级索引中。