1.图的一些基本概念
图是一种非线性数据结构。以下是一些图相关的基本概念:
- 顶点:图中的元素称为顶点。
- 边:图中的每个顶点可以与其它顶点建立链接关系,这种关系称为边.
- 无向图:如果关系是双向的,这种图称为无向图。
- 有向图:如果关系是单向的,就称为有向图。
- 度:每个顶点相连接的边的个数,称为顶点的度。在有向图中度又分为入度和出度。
- 带权图:如果这种关系还是带权重的, 就称为带权图。
2.图的存储方法
2.1 邻接矩阵
2.1.1 存储方法
使用一个二维数组(M)存储图,对于有n个顶点的图,数组的大小是 n * n,数组元素值的缺失值为0。
对于无向图而言,如果顶点 i 和顶点 j 之间有边,则二维数组的元素 M[i][j]的 M[j][i]值都是1。
对于有向图而言,如果仅有一条从顶点 i 指向顶点 j 的边,没有从顶点 j 指向 i 的边,则二维数组的元素 M[i][j]的值都是1, M[j][i]为0。
对于带权图而言,如果仅有一条从顶点 i 指向顶点 j 的边,权重为5,则二维数组的元素 M[i][j]的 M[j][i]值都是5。
2.1.2 优点
方法简单,获取两个顶点的关系效率高(基于数组的随机访问特性)。另外,使用邻接矩阵存储能将很多图的运算转换为矩阵运算,有很多既有的数学研究成果可以借鉴。
2.1.3 缺点
存储无向图和系数图(图中顶点的关联关系较少)的效率比较低。
2.2 邻接表
2.2.1 存储方式
使用一个数组配合多个链表存储。和散列表形式有些相似。某个顶点 i 有边的其它顶点会存储在顶点 i 对应的链表中。
2.2.2 优点
按需存储,节省存储空间。
2.2.3 缺点
由于要遍历链表才能知道两个顶点之间是否有边,所以获取两个顶点的关系的效率较低。这个缺点是有一些优化策略的,比如将链表改为平衡二叉查找树或者跳表提高查询效率。
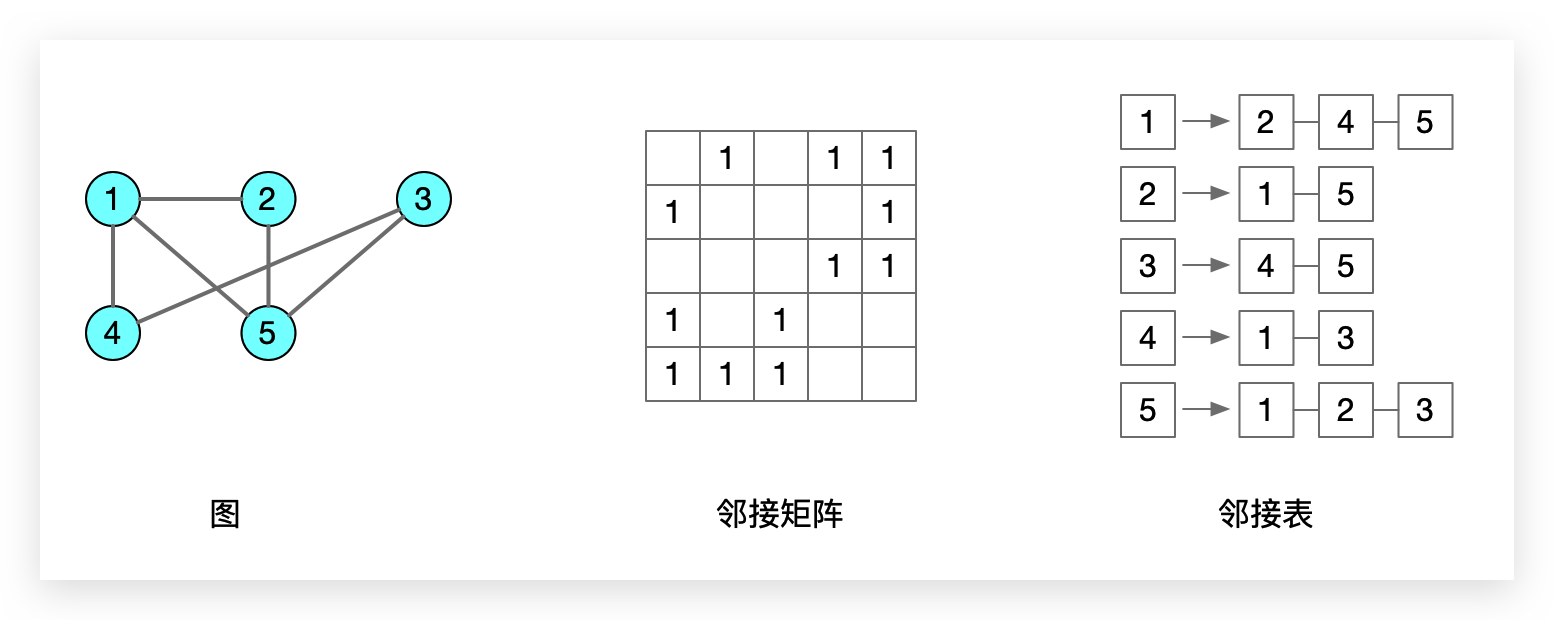
2.3 存储方式图示
3.图的遍历
图的遍历方式最常用的方法有深度优先和广度优先两种方法。
3.1 深度优先遍历 DFS(Deep First Search)
深度优先的大体的思想是,访问某个顶点 a 后,选择与 a 相连的任意一个顶点 b 进行访问,再选择与 b 相连的任意一个顶点 c 进行访问,直至访问的某个顶底不存在与其连接的未访问过的顶点。然后返回到上一层级的顶点,选择另一个未访问的相连节点进行访问,重复过程。
一般采用栈进行辅助,访问完某个顶点后,将其相连的顶点入栈,每次都这样访问并处理栈顶元素,直至栈空。这里有个问题就是重复访问的问题,例如访问 a 后,选择与 a 相邻的节点 b 进行访问,访问 b 后,寻找与 b 相连的节点又会找到 a,造成死循环。所以需要一个辅助的存储空间记录已访问过的节点,来解决该问题。
3.2 广度优先遍历 BFS(Breath First Search)
广度优先的大体的思想是,访问某个顶点 a 后,优先访问和其连接的所有顶点 A(集合),然后再访问和 A 中所有顶点连接的其它顶点。
一般采用队列进行辅助,访问完某个顶点后,将其相连的顶点放入队尾,每次都这样访问并处理队头元素,直至队列为空。这里同样有重复访问的问题,采用同样的方法进行解决。
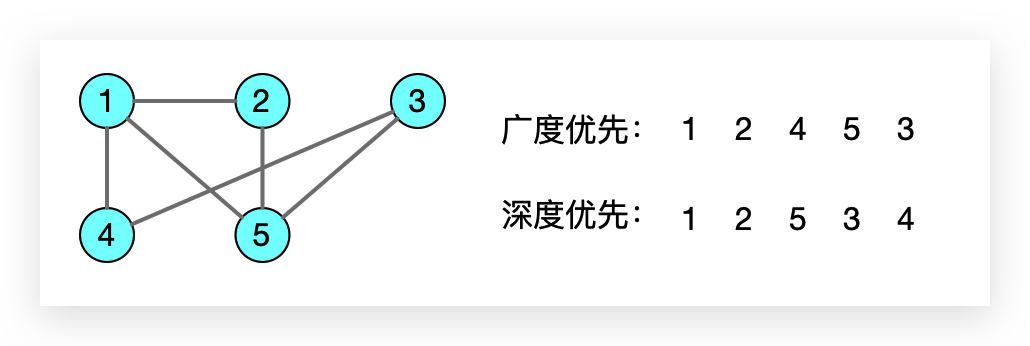
3.3 遍历序列举例
随机选择策略为优先选择值较小的节点。深度优先和广度优先的遍历序列如下: