常用算法:回溯的备忘录优化

发表于 | 分类于

回溯算法的问题

还是以上一篇博客中的0-1背包问题为例，分析回溯算法的决策树。

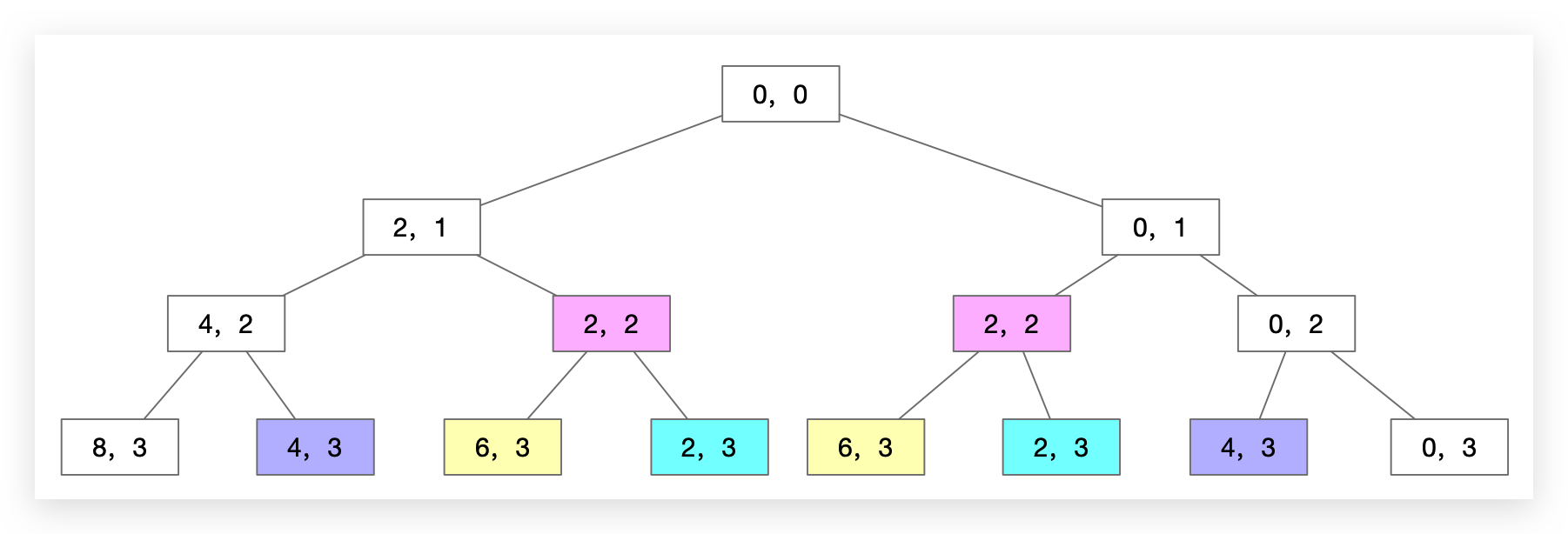
image-20201124210828574

这里只列出了前三层的决策树，可以看到已经有很多状态相同的节点了。这反映出在完整的计算过程中（遍历决策树过程中）包含了大量的重复计算工作。这就是回溯算法不那么高效的主要原因：大量相同子问题的重复计算。

使用备忘录优化回溯算法

如果我们采用某种数据结构把计算过的节点记一下，下次再算某个节点之前判断下这个节点状态是否达到过，如果达到过则直接跳过这个节点接下来的计算过程。这样就避免了大量的重复计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
public class ZeroOneBagWithMemo {
    private int maxWeight = Integer.MIN_VALUE;  //结果放到maxWeight中
    private int[] weight = {2, 2, 4, 6, 2};  //物品重量记录集合
    private int capacity = 9;  //背包容量
    int count = 0;  //节点的处理数量
    private Set<Pair<Integer, Integer>> memo = new HashSet<>();  //备忘录
    /**
     * @param totalWeightNow 当前的累计重量
     * @param step 考察的物品下标
     */
    private void putIn(int totalWeightNow, int step) {
        //通过备忘录查看是否已经计算过改节点
        if (!memo.add(new Pair<>(totalWeightNow, step))) {
            //如果已经计算过则直接跳过
            return;
        }
        //未计算过,走正常的计算流程
        count++;
        //达到总重量 or 已经考察到最后一件商品,则终止
        if (totalWeightNow == capacity || step == weight.length) {
            //终止时比较重量和当前记录的最大值,取大的进行记录
            if (totalWeightNow > maxWeight) {
                maxWeight = totalWeightNow;
            }
            return;
        }
        //选择不放入当前考察的物品,总量不增加,考察下一个物品
        putIn(totalWeightNow, step + 1);
        //选择放入当前考察的物品,先判断是否超限
        if (totalWeightNow + weight[step] <= capacity) {
            //不超限,进行总量累加,考察下一个物品
            putIn(totalWeightNow + weight[step], step + 1);
        }
    }
    public static void main(String[] args) {
        final ZeroOneBagWithMemo zeroOneBag = new ZeroOneBagWithMemo();
        //初始状态,考察第一个下标为0的接口,总重量为0
        zeroOneBag.putIn(0, 0);
        System.out.println(zeroOneBag.maxWeight);
        System.out.println(zeroOneBag.count);
    }
}

记录计算的次数，结果为 21 次。之前未加备忘录的算法为 45 次。可以看到备忘录能大大优化回溯的时间复杂度。

备忘录优化的局限

实际上使用备忘录的回溯算法已经和动态规划有同一数量级的时间复杂度了。那是不是只要掌握回溯算法并用备忘录进行优化就可以了呢？下面看下使用 备忘录对回溯算法进行优化的局限。

升级0-1背包问题：一个背包的总容量是9个单位。几个物品的重量分别为 2、2、4、6、2，价值分别为3、6、2、3、5。选择几样商品装进背包，使得装进背包的物品总价值最大。

先用无备忘录的回溯解决这个问题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
public class ZeroOneBagValue {
    private int maxValue = Integer.MIN_VALUE;  //结果放到maxWeight中
    private int[] weight = {2, 2, 4, 6, 2};  //物品重量记录集合
    private int[] value = {3, 6, 2, 3, 5};  //物品价值记录集合
    private int capacity = 9;  //背包容量
    /**
     * @param totalWeightNow 当前的累计重量
     * @param step           考察的物品下标
     * @param totalValue     当前的累计价值
     */
    private void putIn(int totalWeightNow, int step, int totalValue) {
        //达到总重量 or 已经考察到最后一件商品,则终止
        if (totalWeightNow == capacity || step == weight.length) {
            //终止时比较价值和当前记录的最大值,取大的进行记录
            if (totalValue > maxValue) {
                maxValue = totalValue;
            }
            return;
        }
        //选择不放入当前考察的物品,总量不增加,价值不增加,考察下一个物品
        putIn(totalWeightNow, step + 1, totalValue);
        //选择放入当前考察的物品,先判断是否超限
        if (totalWeightNow + weight[step] <= capacity) {
            //不超限,进行总量累加,价值进行累加,考察下一个物品
            putIn(totalWeightNow + weight[step], step + 1, totalValue + value[step]);
        }
    }
    public static void main(String[] args) {
        final ZeroOneBagValue zeroOneBag = new ZeroOneBagValue();
        //初始状态,考察第一个下标为0的接口,总重量为0
        zeroOneBag.putIn(0, 0, 0);
        System.out.println(zeroOneBag.maxValue);
    }
}

以上面的算法绘制决策树：

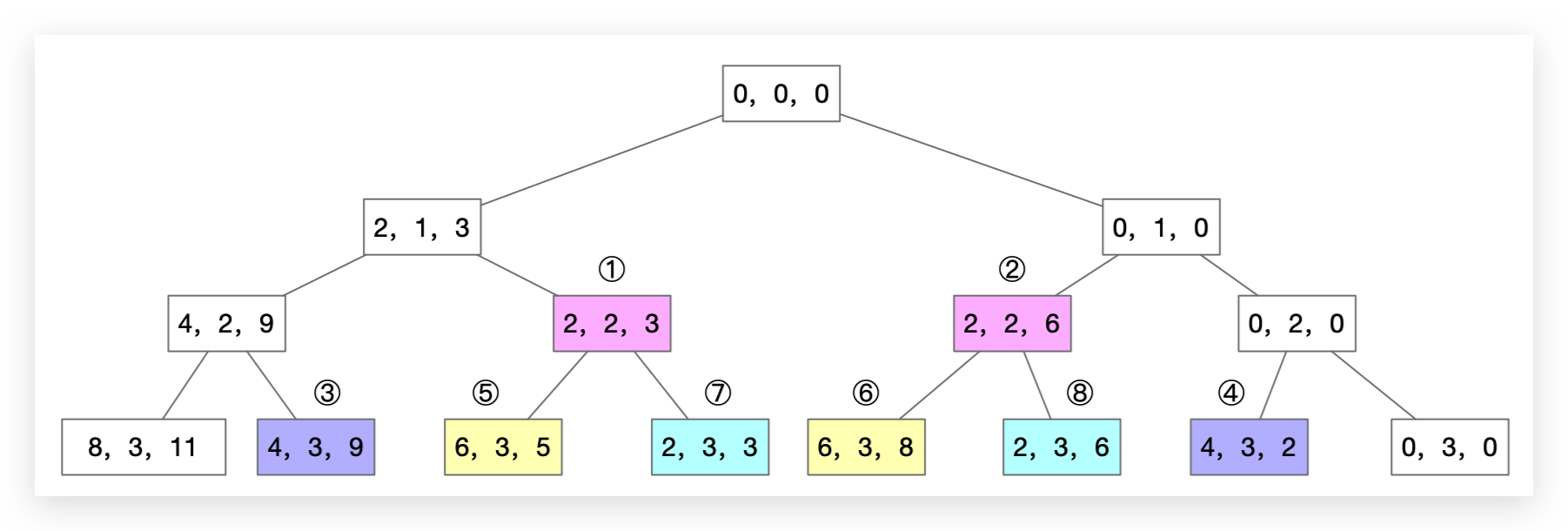
image-20201126112018365

可以看到每个节点含有三个变量（a，b，c）。但判断方式不再是a,b,c三个变量都一样时，放弃后面的计算。而应该是：如果遇到（a，b，c）节点，发现之前已经计算过（a，b，c’）,且 c < c’，则可以进行剪枝直接放弃（a，b，c）。所以备忘录不是不能用，而是判断的规则要复杂一些，需要比较价值积累。正是这个策略使得备忘录不再那么高效。

以上面的决策树为例：先计算完①节点，并不能指导我们放弃②的计算，因为6 > 3。⑤⑥、⑦⑧同理，只有在③④节点的计算上是奏效的。生效的节点对就是1对，不生效的是3对。这样备忘录模式就不是那么高效了。

但如果我们决策树的遍历先进行右子树，那么生效的节点对就是3对，不生效的是1对。

如何优化

如过对上述决策树的遍历是广度遍历，即一层层的遍历，完成一层所有节点的状态确定后再往下一层。那么遍历完第三层所有节点后，对比各个节点的状态，就可以将①号节点抛弃掉。就能避免因深度优先的遍历顺序造成剪枝失败的问题。

这种思想就是动态规划。