常用算法:动态规划

发表于 | 分类于

使用动态规划解决升级的0-1背包问题

上一篇博客提到，适用备忘录优化的回溯算法并不能很好的优化升级的0-1背包问题，下面我们看看动态规划是如何高效的解决问题的。

问题：一个背包的总容量是9个单位。几个物品的重量分别为 2、3、1、4、3，价值分别为3、6、2、3、5。选择几样商品装进背包，使得装进背包的物品总价值最大。

解决这个问题，一共需要做5步决策（最多），背包总容量是9个单位。我们建立一个5 * 10（9+1）的二维数组 T 来记录状态。

二维数组的元素 T[m][n] = v 表示，已经考察完了前 m+1 和物品，累计总量为 n，总价值为v。T[m][n]的值可以由T[m-1][n]结合物品总量和价值数组得到。针对得到的多个v的值，我们选择较大的作为最终的状态值。

当这个状态记录矩阵完成填写后，其中所有元素的最大的值即为最大的价值数。

下面画出整个状态记录数组的状态转移过程。最终的最大值为16。

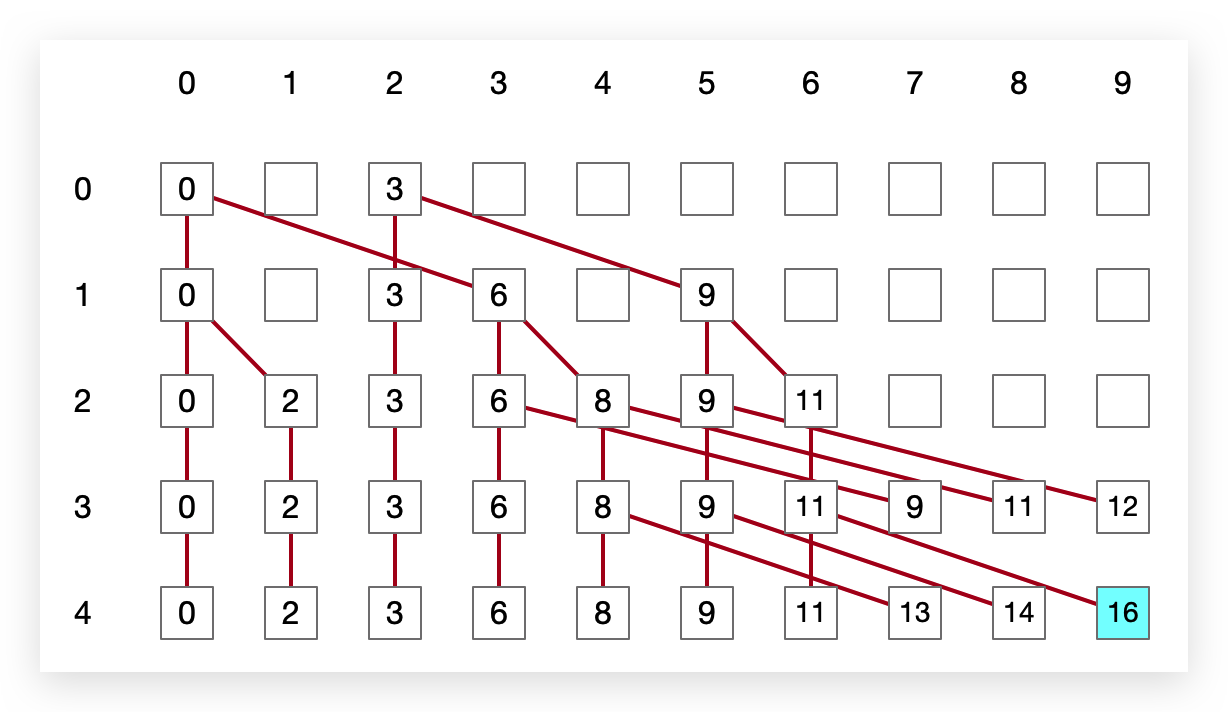
image-20201128114413428

将如上的状态计算过程用代码表示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
public class ZeroOneBagValueDynamic {
    private int maxValue = Integer.MIN_VALUE;  //结果放到maxWeight中
    private int[] weight = {2, 3, 1, 4, 3};  //物品重量记录集合
    private int[] value = {3, 6, 2, 3, 5};  //物品价值记录集合
    private int capacity = 9;  //背包容量
    //状态记录矩阵
    private int[][] status = new int[weight.length][capacity + 1];
    private void caculate() {
        //状态记录矩阵值初始化
        for (int i = 0; i < status.length; i++) {
            for (int j = 0; j < capacity + 1; j++) {
                status[i][j] = -1;
            }
        }
        //第一次决策数据初始化
        status[0][0] = 0;
        if (weight[0] <= capacity) {
            status[0][weight[0]] = value[0];
        }
        //第二次决策往后依次进行决策
        for (int i = 1; i < status.length; i++) {
            for (int j = 0; j < capacity + 1; j++) {
                //上一步status序列某个值为初始值-1,则略过
                final int statusValue = status[i - 1][j];
                if (statusValue == -1) {
                    continue;
                }
                //上一步status序列某个值为不为初始值,基于这个值计算当前status序列
                //当前决策选择不装入物品
                final int max = Math.max(status[i - 1][j], status[i][j]);
                status[i][j] = max;
                //记录最大值
                maxValue = Math.max(maxValue, max);
                //在判断装入后不会超过背包容量时,决策选择装入物品
                if (j + weight[i] < capacity + 1) {
                    final int max1 = Math.max(status[i][j + weight[i]], status[i][j] + value[i]);
                    status[i][j + weight[i]] = max1;
                    //记录最大值
                    maxValue = Math.max(maxValue, max1);
                }
            }
        }
    }
    public static void main(String[] args) {
        final ZeroOneBagValueDynamic zeroOneBagValueDynamic = new ZeroOneBagValueDynamic();
        zeroOneBagValueDynamic.caculate();
        System.out.println(zeroOneBagValueDynamic.maxValue);
    }
}

最后输出与上述结论一致：16。

动态规划适用范围

多阶段决策最优解模型：一般是用动态规划来解决最优问题。解决问题的过程需要经历多个决策阶段。每个决策阶段都对应着一组状态。然后我们寻找一组决策序列，经过这组决策序列，能够产生最终期望求解的最优值。

特征一：后面阶段的状态可以通过前面阶段的状态推导出来。

特征二：在推导后面阶段的状态的时候，我们只关心前面阶段的状态值，不关心前面状态是怎么一步一步推导出来的。某阶段状态一旦确定，就不受之后阶段的决策影响。

特征三：不同的决策序列，到达某个相同的阶段时，可能会产生重复的状态。